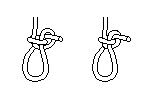↑↑ Home ↑ Science

Knotty topics

Knot physics -- The winding number -- The trucker's hitch -- An unnamed loop -- Links

Knot physics

There are a number of web sites dedicated to knot tying and some about knot theory, but none (to my knowledge) that tries to connect the two. Since it is the subject of physics to describe real-world phenomena with mathematical means, this can with some justification be called knot physics.

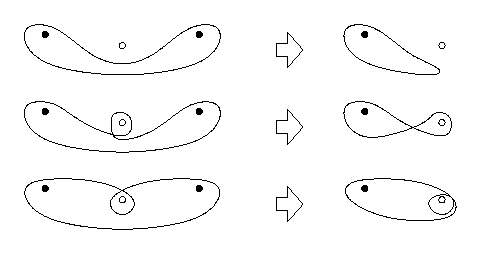
Take for instance identifying common knots with in the mathematical classification. Mathematical knots are tied on a closed loop, while most knots in the real world aren't - most of them would be impossible to tie that way. To compare knots to the classification, one has to join the ends of the rope after tying the knot.

Those knots that can be tied "in the bight", ie without access to the ends of the rope, could also be tied in a loop of rope without cutting and rejoining it. Therefore all of them are equivalent to the unknot, the unknotted loop. Among them are the sheep shank, the boa and the constrictor knot and many loops and hitches. Two further knots whose classification is well-known are the overhand knot (trefoil to mathematicians) and the figure-8 knot. The following table contains a few more:

Overhand knot31
Figure-8 knot41
Double overhand knot51
Bowline63
Unnamed loop (see below)51
Necktie knot31
Windsor knot (for neckties)01 (unknot, when your neck isn't in the way)
Reef, thief and granny knotdouble 31 (in different orientations)
Grief knot31 (only one!)
Hangman's noose01 (so long as nobody's neck is on the line)
Buntline hitch31 (only one, contrary to what I said here earlier)
Tautline hitch31 # 51
Anchor bend (really a hitch)31 # 51
Karate belt knot31 # -51 (after taking the Karateka out first)

The trucker's hitch is a bit of a speciality. One can choose one of several loops to tie it, one can slip the loose end through the loop from back to front or from front to back, and including the half hitches further complicates an already complicated knot. I will do without the half hitches and just tie the loop and join the ends of the rope after putting one through the loop. There remain two versions for each type of loop. Here's the list of the trucker's hitch variants I tried out:

with slipped overhand knot62 or 63
with slipped figure-8 knot76 or 77
with in-line figure-8 knot76 or 945

It gives me heart that the variant I use (see below) is the most complex of them - it is quite obviously superior ;).

Then there are knots for joining ropes together, called bends. After joining the two ends of both ropes, they can be classified as links.

Reef knot021 (mathematical proof that it is useless as a bend ;) )
Sheet bend (both normal and doubled)221
Full carrick bend827
Zeppelin bendconnected sum of two 221 and two differently-oriented 31

Since I first did these classifications, the task has become rather easier. There is a classification web application at the Indiana University's KnotInfo site which works at least for prime knots. Otherwise you have to look at a knot table and transform your knot until you can match part of it.

Belay stations, the winding number, and links

If you find yourself at a belay station in the middle of a rock wall where there are two bolts which you want to use both for redundancy, you never secure yourself as shown on the left-hand side of the picture below. (And incidentally, you don't do a dangerous sport like rock climbing unless and until you have learned it from an experienced instructor. Reading web pages is definitely not enough.) Rather, you twist the upper part of the webbing into an additional loop as shown on the right-hand side and put the karabiner linked to your climbing harness through it.

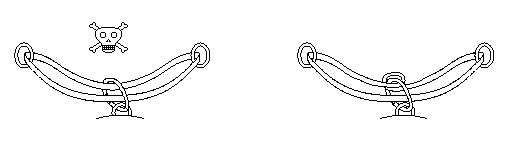
The reason is perfectly clear to any topologist: On the left, the winding number of the webbing loop with respect to any point of the carabiner is zero, while on the right, it is one with respect to the point where the carabiner passes through the small loop. In the language of knot theory, the webbing and the carabiner form the unlink 021 on the left, but the link 221 on the right. In the language of rock climbing, that means that if you forget the additional twist and one of the bolts fails, you have a problem.

One might think that it doesn't make a difference to twist the webbing into a loop towards rather than away from oneself. That would be no catastrophy, but it is not quite the same: The winding number is now two, and the link 421 is formed. The upshot is that the webbing wraps around the karabiner twice, which creates a bit of a muddle should one bolt fail. Therefore it is not usually done that way.

Here is an illustration of how to read off the winding number, including a sketch of the Murphy scenario. Identifying the link classification number requires a table of links (such as one of these) and a little spacial imagination.

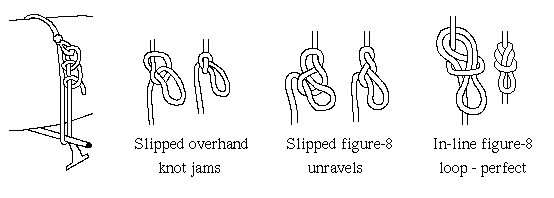
My variant of the trucker's hitch

I've been using the trucker's hitch frequently to fasten kayaks on roof racks and found part of it - the loop - impractical. As the width of the load (ie the number of kayaks) varies, one has to untie and retie it in a different position. Haven't the countless truckers and knot book authors noticed that the slipped overhand knot which customarily forms the loop is near-impossible to untie once it has been used for some time? Ok, the problem doesn't occur if you undo and retie the knot every time you use the roof rack, but who does? I've searched the web for a different version but all knot sites display it with either the slipped overhand knot or (a few) with the slipped figure-8 knot.

The slipped figure-8 knot doesn't jam but has some problems of its own - it gets untied easily if one pulls the lower end of the rope too much. One day I came across the in-line figure-8 loop at the Knot Knowledge site (which has now vanished). It doesn't jam, nor does it untie itself when one pulls the hanging part of the rope. All parts of the rope curve towards the direction of their load along gentle loops. This seems to be a very strong knot.

It has some slight disadvantages. It is tightened mainly by pulling the standing part (ie upper part) of the rope, which means it will end up lower than where you started tying it. You can't untie it just by pulling the hanging part. Besides it is not easy to tie one-handed. This is sometimes necessary for making the loop some way up the rope on top of a large van. Being right-handed, I tie the mirror-image of the one from Knot Knowledge, as shown below.

An unnamed loop

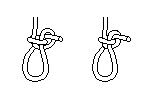
This loop serves as a decoration in a restaurant in the baltic spa of Kühlungsborn. I have got no idea how widely known or used it is, but have found it nowhere else. In fact it doesn't even seem to be in the Ashley Book of Knots, which would mean it's probably been brought to us by aliens (or else I didn't look closely enough). It seems to be easy to untie and rather insecure, but is strong and doesn't jam when pulled. Its mathematical classification is 51.

Knot links

TOS / Impressum